The average bend radius of a tube is a fundamental parameter in feasibility calculations for the bending of tubes, pipes and structural sections. The average bend radius corresponds to the centreline radius (CLR): also termed the neutral line, this is an imaginary line drawn through the middle of the tube.
In this article, we take a closer look at the formulas and calculations needed to determine tube bending feasibility, which use values for the bend radius, tube thickness and the K-factor.
Feasability formulas for tube bending
- Average bending radius
- Pipe diameter
- Thickness of the tube
Interpreting the K-factor
The K-factor is calculated based on value ranges and is used to determine the following:
- Tube bending feasibility (whether it is in fact possible to bend a round, square or rectangular tube)
- Predicted difficulty of tube bending
Feasibility of bending round steel tubes

To assess the feasibility of bending round steel tubes, the ratio of the average bend radius to the diameter and the thickness of the affected tube is considered.
The formula is as shown below:
- CLR = Centreline radius
- WT = Wall thickness
- OD = Outer diameter
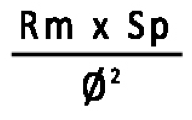
This formula produces the value for the K-factor.
The difficulty of the tubing bending is inversely proportional to its value: the difficulty increases with a low K-factor and decreases with a high K-factor.
- K > 0.30 – Bending the tube is more ‘straightforward’ and there is now need to use special support jigs that would need to be manufactured ad hoc.
- 0.30 > K > 0.10 – The bending process is of normal difficulty: using only an internal, fixed bending mandrel will be sufficient.
- 0.10 > K > 0.08 – A fixed bending mandrel with a wiper die – a special tool to restrict tube deformation – will be needed for bending the tube.
- 0.08 > K > 0.05 – Tube bending is possible only when using a movable, internal mandrel in conjunction with a wiper die.
- K < 0.05 – The tube cannot be bent under normal conditions. In this case, tests must be run in order to evaluate whether the K-factor can be reduced and if special bending jigs need to be constructed.
To verify the feasibility of bending round steel tubes, the ratio between the average bending radius, diameter and thickness of the tube concerned is considered.
Feasibility of bending square or rectangular tubes
The formula for calculating the feasibility of bending square or rectangular steel tubes differs slightly to the formula that is used for round tubes.
The formula is as shown below:
- CLR = Average bend radius
- WT = Wall thickness
- F = First side of the tube (square/rectangular)
- S = Second side of the tube (square/rectangular)
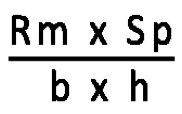
As with round tubes, we determine the feasibility and difficulty of the bend based on certain intervals of K-factor values:
- K > 0.20 – A fixed mandrel is sufficient for bending the tube.
- 0.20 > K > 0.15 – A movable mandrel is required to bend the tube.
- 0.15 > K > 0.10 – Bending the tube requires the use of a fixed mandrel with a sliding block.
- K < 0.10 – In theory, it will not be possible to bend this tube. Tests must be conducted to lower the level of difficulty.
Calculating the K-factor when bending a tube made from stainless steel and aluminium
The formulas that we have seen above are used to determine the feasibility of bending tubes made from steinless steel. When bending tubes made from stainless steel and aluminium, which have a range of different properties, the K-factor is lower:
- Stainless steel SAE 304 -> reduce K by about 20%
- Stainless steel SAE 316 -> reduce K by about 25%
- Aluminium 6060 -> reduce K by about 35%
As can be seen from the above example, bending a tube made from stainless AISI 316 steel is harder than bending a tube made from alloyed 304 steel, since the former has greater compressive strength than the latter. This means that the bent stainless tube often shows ‘wrinkles’ on the inner surface of the bend. The K-factor for stainless steel (AISI 316) is indeed smaller than the value for AISI 304 small. Bending aluminium is even more complex, since aluminium is less ductile than steel. For this reason, the K-factor is reduced by about 35%.
Structural sections: how do we calculate the feasibility of a bend?
Metal tube ductility: what it is and why it is important
To identify the overall length of the bent tube, including its straight parts, a precise calculation of the change in the tube’s length must be made.
The formula to calculate the resultant length of a bend is as follows:
- OD = Outer diameter
- π = Pi
- CLR = Bend radius

The tube is stretched as it bends. This elongation can have the following consequences:
- Tube breakage
- Lack of tube bending precision
To calculate the exact length of the bend, the product of the above formula must therefore be divided by another coefficient – known as the coefficient of elongation. This value will vary depending on tube diameter and wall thickness, as well as the average bend radius and alloy percentages.
A Ø30 x 2 mm steel tube with the same radius as a Ø30 x 2 mm aluminium tube will nonetheless have a different coefficient.
The value for the length of the tube bend is also important for determining the exact point at which the laser cut needs to be made, as well as the length of this cut. Calculating the laser cutting position incorrectly means that the resulting bent tube will be longer or shorter than it should have been. If the tube is longer and cannot be cut, this incorrect calculation of the laser cutting position has resulted in irreparable damage to the entire tube processing procedure.

More information:
Importance of cast metals for tube bending
In cases where a metal pipe has been produced by using various pieces of cast metal, calculating the coefficient of elongation is much more difficult and can cause problems when bending the tube. This problem occurs in particular if the metal tube is delivered directly from the customer, who may often lack the experience necessary in order to verify the alloy quality.
To ensure high quality during tube processing and ensure higher rates of throughput for the overall production process, the metal tube should have been manufactured from a single piece of cast metal. This is why we always take steps to ensure that tubes are produced from a single cast.

Summary
The K-factor is decisive for determining the feasibility of the bend process. The bend radius of the tube must be known in order to calculate this value.
However: we should not overlook the fact that this is always only a theoretical value. When cold forming a tube, there are many other variables to consider that may affect the outcome of the bending process.
The 3D software provided by modern CNC tube bending machinery is an important tool for ensuring the success of tube processing.
As is the experience and expertise of workshop staff and the team in the technical performance tube bending unit at Tecnocurve.
IMPORTANT NOTE: The formulae given are a simplification of a much more complex calculation system. Our aim was to give the reader a rough guide to calculating the feasibility of bending a tube. For more detailed information on calculating the feasibility of bending a tube or metal profile, please contact our technical department directly.